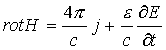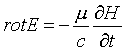Электромагнитное поле

В 1931 году, почти одновременно с открытием электромагнитной индукции Фарадея, в семье шотландского лендлорда Джона Клерка Максвелла родился сын Джеймс. Он рос, а открытия Фарадея начали получать широкое применение, «старик пар» начал сдавать «великому революционеру» - электрической искре.

Вместе с отцом он часто посещал заседания Королевского общества, на одном из них встал вопрос, каким образом древние этруски вычерчивали правильные эллипсы. Четырнадцатилетний мальчуган, Джеймс предложил остроумный и гениально простой способ с использованием двух иголок и связанной в кольцо нити. Способ был с успехом принят членами Королевского общества.

Двадцатилетним, Максвелл познакомился со своей ровесницей - теорией Фарадея «Экспериментальные исследования» произвели неизгладимое впечатление. «Я решил, – писал он, – не читать ни одного математического труда в этой области, покуда не изучу достаточно основательно «Экспериментальных исследований по электричеству». Любовь была с первого взгляда и на всю жизнь.

К фарадеевской концепции «поля» Максвелл присоединяется безоговорочно. Нравятся ему и силовые линии Фарадея. Максвелл видит, что Фарадей постепенно отходит от силовых линий как геометрических символов ко вполне реальным силовым линиям, обладающим, например, упругостью, стремящимся пойти по кратчайшему пути, отталкивающимся друг от друга.

Для получения математических закономерностей он использует метод построения аналогий, имеющих вид реальных объектов. В этих моделях, он рассматривает электрическое поле в виде потоков некоторой жидкости, задавая характеристики этой жидкости, он пытается понять ее поведение и отыскать законы функционирования. Таким образом, для электрической жидкости он получает закономерности, идентичные формулам электростатики, подтверждая тем самым идею силовых линий.

Похожим образом он поступает и для случая постоянных магнитов, магнитное поле вне их изображается, как электрическое поле электрических зарядов. Внутри же магнит разбивается на элементарные магниты, и каждый рассматривается как исток и сток воображаемой жидкости.

Эти модели электрического и магнитного поля дают возможность выразить представления Фарадея на математическом языке и представить известные закономерности электродинамики, исходя из принципа близкодействия. При этом “шлифуя” математические связи он вводит ряд новых понятий – величин, которые являются функциями точек пространства. Это напряженность и индукция магнитного и электрического полей, поток напряженности и индукции полей, вектор-потенциал, а также плотность электрического тока.

Однако, эти представления не могут объяснить рождение электромагнитной индукции, как явления единого электромагнитного поля. Нужна была другая модель, которая была построена Максвеллом в работе «О физических силовых линиях».

Максвелл опять рассматривает пространство, заполненное воображаемой жидкостью. В этой жидкости образуются вихревые трубки, которые контактируют между собой промежуточным слоем, представленным небольшими шариками. Вращение трубочек может вызвать перемещение шариков, чье движение также вызывает закручивание соседних трубок. Вихревые трубочки представляющие магнитные силовые линии, а маленькие шарики являются электрическими частицами. Тем самым электрическое и магнитное поле оказывается взаимосвязанным.

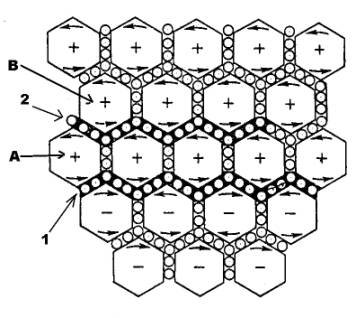
Большие шестиугольники - это вихревые трубочки представляющие магнитные силовые линии, а маленькие шарики являются электрическими частицами.

Пусть некоторый слой электрических частиц «1» приходит в движение слева направо под действием некоторой силы – это означает, что в слое действует электродвижущая сила, вызывающая электрический ток. В результате движения частиц в слое «1» близлежащие слои вихрей начнут вращаться. Таким образом, вокруг тока возникнет магнитное поле. С вихрями слоя «А» сцеплены электрические частицы слоя «2» на них также начнет действовать сила, и возникнет электрическое поле.

Если частицы находятся в проводнике, то они придут в движение при этом появится электрический ток проводимости. Если частицы находятся в диэлектрике, то они не могут двигаться, но могут сместиться из положения равновесия на некоторое расстояние. В этом случае ток проводимости не возникает, но возникает ток смещения.

Движение частиц в слое «2» вызывает вращение вихрей в вихревом слое «В», и когда скорости вращения вихрей «А» и «В» сравняются движение частиц электрическом слое «2» прекратится. Тем не менее, возмущение, вызванное электрическим полем в слое «1» будет передаваться слою «А» затем «2» от него «В» и так далее - «3» - «С» - «4» - «D» - перемещаясь, таким образом, в пространстве. Если на пути попадаются проводники, то в них возникают кратковременные токи индукции.

Поведение своей абстрактной математической конструкции он подвергает математическому анализу, он получает уравнения электромагнитного поля. Их написанию он посвятил большую часть своей жизни, уравнениям, которые позже стали называться «уравнениями Максвелла».

Уравнение:

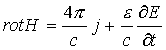
говорит о том, что вектор напряженность магнитного поля Н вращается (функция rotor – вихрь) вокруг полного тока, равного сумме тока проводимости:

за счет носителей заряда
и тока смещения

Уравнение:

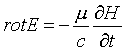
говорит о том, что с изменением напряженность магнитного поля Н вокруг этого вектора (Н), начинает циркулировать вектор электрического поля Е, причем в направлении (знак « - »), в котором происходит подавление поля Н.

Уравнение:

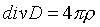
говорит о том, что источником электрического поля являются электрические заряды r в рассматриваемом объеме. Здесь D – вектор электрической индукции (смещения), а функция div – описывает источник, вернее его мощность. Так если взять кольцо маленького диаметра то, мощность костра можно оценить как массу дыма, проходящего через это кольцо за одну секунду.

Уравнение:

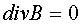
говорит о том, что нет источников магнитного поля (магнитных зарядов), а линии вектора магнитной индукции, образуют замкнутые окружности.

Уравнения были просты, но чем больше Максвелл и его последователи над ними работали, тем больший внутренний смысл находили в четырех строчках. Генрих Герц, знаменитый немецкий физик, роль которого в истории – доказать полную справедливость представлений Максвелла, писал о неисчерпаемости теории Максвелла. Замечание Генриха Герца о «самостоятельной жизни» уравнений Максвелла, о том, что они «умнее самого автора», стало подтверждаться сразу же после того, как Максвелл начал изучать свою систему, пробовать на решении различных задач.

Помимо векторов, описывающих электрическое и магнитное поле, в уравнения входили некие константы, а именно e, m и с. Первые две - e и m - были названы диэлектрическая и магнитная проницаемости среды соответственно, они характеризовали влияние среды на прохождение электрических и магнитных полей, и для каждого конкретного случая их было необходимо находить экспериментально. В будущем им еще предстояло сыграть свою роль, но сейчас Максвелла больше интересовала третья константа – с, что это такое?

Применив уравнения к одному конкретному случаю, Максвелл нашел, что неизвестное число c оказалось примерно равно 300 000 километров в секунду!

Совпадение было слишком изумительным, чтобы не принять его во внимание. Таинственное c было равно скорости света? Но при чем тут скорость света? Максвелл настолько глубоко верил в свои уравнения, что наличие физически не очевидного коэффициента его беспокоило. Он непрерывно думал о странном явлении. И уравнения «думали».

Согласно первому уравнению, переменный ток создает вокруг себя изменяющееся магнитное поле, это переменное магнитное поле (согласно второму уравнению) уже в следующем элементе пространства создаст электрическое поле, электрическое поле создаст магнитное, магнитное – электрическое, и так до бесконечности.

Причем эти поля могут перемещаться в среде, где нет носителей заряда (гениальная догадка Максвелла ввести ток смещения), в этом случае распространение электромагнитного поля описывается волновым уравнением, содержащим постоянную « с » в качестве скорости распространения.

Другими словами, электромагнитное поле, как с поразительной ясностью понял Максвелл, распространяется в виде «поперечной» волны, причем волны незатухающей – энергия магнитного поля в пустоте полностью переходит в энергию поля электрического, и наоборот. Но ведь в виде точно таких «поперечных» волн распространяется и свет, таким образом «свет есть электромагнитное возмущение».

Идеи Фарадея наконец-таки, обладали не только физической сущностью, но и приобрели математическую форму, однако принимать их не спешили. Исследования Фарадея и Максвелла были бунтарскими, наносящие безжалостные удары по учению Ньютона. Сначала оба названных выше создателя новой теории отвергли силы мгновенно оказывающих свое действие на расстоянии, утверждая, что электромагнитные явления передаются при помощи возмущения некоторой среды – эфира. Второй удар был нанесен по материальным точкам, которые в соответствие с теорией Ньютона были единственными носителями энергии; в новой теории - поле, наделенное энергией, выступает как физическая реальность. Поэтому трактат Максвелла больше походил на театр военных действий, на более чем тысячи страницах «он был загроможден следами его блестящих линий нападения, его укрепленных лагерей, его битв». Сложная книга, самим уравнениям непосредственно было посвящено несколько десятков страниц, они были разбросаны по всей книге, и их было довольно много – 12.

Во всех уравнениях Максвелла необходимо было разобраться, выделить из них лишь основные и привести их к единственному, «исходному» виду. Работу по «расчистке» «Трактата» Максвелла провели Густав Герц и Оливер Хевисайд.

Более того, нужно было доказать само существование тока смещения и единого электромагнитного поля, свободно перемещающегося в пространстве. Сам Максвелл к экспериментальному их доказательству явно не проявлял интереса, довольствуясь абстрактной математической моделью.